CITS2002 Systems Programming

Lecture & Workshop
recordings on LMS

Schedule

FAQ

Unit outline

C textbooks

OS textbooks

Information resources

Look after yourself!

Workshop 3: Functions, parameter passing, and structures

BEFORE this workshop session, you're strongly encouraged to think how you would do it. You are not expected to have developed and tested a perfect solution before the workshop, but you should at least scratch out your approach on paper.

In this workshop we'll develop a small number of functions to determine the distance between two points on the Earth's surface.

We'll first develop a command-line utility, named haversine, that accepts a pair of points on the Earth's surface and determines the distance between the two points:

prompt> ./haversine -31.977537 115.816451 -31.982842 115.818725 627metres

We'll next develop a utility, named haversine2, that accepts an arbitrary number of latitude and longitude pairs, and determines the distance between the first and last points (by following a route):

prompt> ./haversine2 \ -31.977537 115.816451 -31.977632 115.816871 \ -31.977616 115.817170 -31.980981 115.817174 \ -31.980975 115.818709 -31.982842 115.818725 796metres

There are number of formulae that perform this calculation, some accounting for the fact that the Earth is not a true sphere.
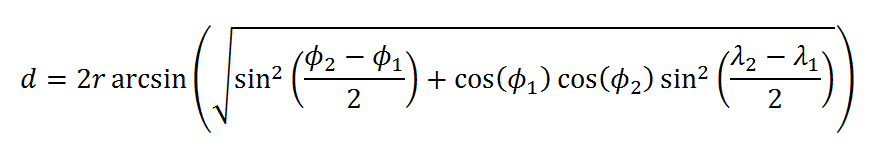
One of the simplest is haversine's formula [Wikipedia]. We are interested in the simplified formula from Wikipedia:

NOTE - this workshop is not requiring us to understand the formula, just to implement it in C11. Do not be alarmed by the use of spherical trigonometry (it won't be in the exam!)

The haversine function was used in the CIT2002 1st project from 2015.

Our goal is to:

design a C11 structure to represent a point on the Earth's surface,

to develop 3 simple functions:

double degrees_to_radians(double degrees);
bool valid_location(struct point location);
double haversine(struct point location1, struct point location2);

and to use them, in combination, to calculate the distance between the Computer Science building and the ~~Tavern~~ Barry J Marshall Library.

BEFORE the workshop session, you're strongly encouraged to think how you would do it. You are not expected to have developed and tested a perfect solution before the workshop, but you should at least scratch out your approach on paper.

From the information presented in lectures so far, we know:

variables in our programs have a datatype which describes the meaning and (internal) representation of the variable's possible values.
functions are named sequences of statements, that are either called to calculate a value, or to 'produce' a side-effect.
functions receive zero or more parameters which provide input(s) to the function, or control its execution.
like variables, function parameters also have a datatype (in fact, during the execution of each function, its parameters act like local variables).
functions may return a single value, which also has a datatype, and this returned value may be used in further calculations, or printed...
Functions of type void return no value.

So, before the workshop session, think how you can combine this (already known) information to develop a solution.

How can we TEST it?
🌶 For what values would the simpler formula $\sqrt{Δx2+ Δy2}$ be accurate enough?

And a great article on very early attempts to calculate the Earth's radius: https://www.abc.net.au/.../eratosthenes-measured-circumference-of-the-earth-2200-years-ago.