Tetris

1. The board is a semi-infinite rectangle of width w units, with the open end upwards.

2. There are seven distinct pieces, each a contiguous block of four equal squares, each of side 1 unit. The pieces are known as tetrominoes. (Pieces and their representations are described below.)

3. n pieces are delivered in a sequence from the open end of the board.

4. The player has a buffer that can hold up to b pieces at one time.

5. Denoting the next unprocessed piece in the sequence by X, at a typical moment in the game the player has 1-3 options:
   • place X onto the board; or
   • if the buffer is not full, add X into the buffer; or
   • if the buffer is not empty, place any piece from the buffer onto the board.

   The first two options consume X: the third option does not (i.e. X is still the next unprocessed piece).

6. Placing a piece onto the board involves four steps, which we will view as happening in this order:
   1. rotate the piece 90r degrees anti-clockwise, where r is an integer in 0 .. 3; then
   2. locate the piece k units from the left wall, where k is an integer in 0 .. w-1 (but the piece cannot protrude outside the right wall); then
   3. slide the piece downwards until some part of it collides either with the bottom wall or with some part of a previously-placed piece; then
   4. for all lines across the rectangle which are completely full of squares, delete those lines and slide all higher squares down accordingly.

A Wikipedia page exists which discusses Tetris. There are many, many Tetris games available online, for example at tetris.com.

Pieces and their representation

   1     2      3      4       5       6      7

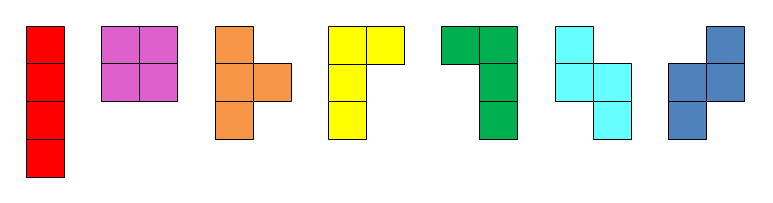
An instance of the problem is described by a text file where all characters in 1 .. 7 denote pieces, and all other characters can be ignored, for example exampleinput.txt.

A placement of n pieces is described by a text file (like exampleoutput.txt) containing n lines. Each line has the form x y z, where x, y, and z are all integers and

• 1 <= x <= 7  denotes a piece to be placed,
• 0 <= y <= 3  denotes an anti-clockwise rotation of that piece by 90y degrees (so 0 denotes the orientation shown above), and
• 0 <= z          denotes that the rotated piece should be dropped z units from the left wall (any z which is too big will leave the rotated piece touching the right wall).

The placement file exampleoutput.txt gives this final board, where "up" is pointing rightwards. The files h001.svg - h014.svg show the partial placements of these pieces: three lines were cleared, one each after the 9th, 14th, and 15th pieces.

Each output file will be checked for legal syntax and for consistency with the corresponding input file (i.e. that it places the pieces in a legal order).

Submission

• Initally, you can assume that w = 11, b = 1, n <= 1,000. If you are able to generalise your system beyond these values (or even to pieces with five squares!), that would be great.
• Aim for a system that can process maybe 5-10 pieces per second.
• More example data will be available from here in due course.

You must submit two deliverables via cssubmit:

• the code you generate in the project, as a zip archive; and
• a paper describing and analysing your work, as a PDF file.

The paper should be about 5-10 pages long: it should describe the structure and design of your program, and include any (experimental or theoretical) analysis that you have performed.

If you use or refer to other people's work, make sure that you give all due credit.

Analysis and assistance

1. This is a Python program that can be used to generate input files of the type described above. The program expects an input file where the first line specifies the number of pieces to generate, and the next seven lines specify the relative frequencies of the seven piece-types (except that negative numbers are treated as zeroes).
2. The question has been raised on help4211 whether to implement the "Original algorithm" for gravity, or the "Chain reactions" algorithm, as per the Wikipedia page. The answer is the Original algorithm, although feel free to implement both and discuss/compare them in your report.
3. I will post more input data and output data here in due course, but feel free to make up your own.
4. Here is a Python program DrawPlacement.py which reads in a placement file and produces a sequence of svg files, of the type shown above. Just run it and give it a filename. It does no error checking and it may be buggy: if you find a bug, let me know. Here is the Haskell version. If someone knows an easy way to animate these svgs, please let me know.
5. The seven pieces have an average of 2.7 distinct rotations, and for w = 11, an average of about 26 distinct placements. Thus even if b = 0, n given pieces generate roughly 26 ^ n distinct output sequences (although clearly not all of them generate distinct placements). With a non-zero buffer, this number is much higher. It's a hard problem!

Assessment

You may decide how to distribute the various project tasks (for example programming, testing, collecting empirical data, producing plots, writing, etc) between the group members, but the marks will be divided evenly, so the workload should be roughly equal too.

The project counts for 25% of your mark for CITS4211. Assessment will be based on

• how well you have used the AI algorithms that we have studied,
• how well you have analysed the problem,
• how well you have analysed your program,
• how well your program plays Tetris,
• how well your paper is written,
• and anything else that occurs to me at the time.

You should consult the School's guidelines on plagiarism, available from the unit outline.

Deadline

Standard penalties will apply for late submission, as specified in the unit outline.

Prize competition

1. These are the initial data files: equal-1000.txt, soz-1000.txt, joil-1000.txt, soz-equal-2000.txt, joil-equal-2000.txt.

2. Run your submitted program on each of the data files. Use a width of 11 and a buffer-size of 1.

3. Email the output files to Lyndon by the end of 14 June.

4. Any illegal output files will result in immediate ejection from the competition.

5. The files will be compared only by the height of the final boards.

6. If two or more programs' performance is close, I will post more data here and announce it on help4211, and on this page.

Lyndon's decisions are final.