Physical Layer responsibilities:

• Provides the physical topology of the network
• Provides the transfer medium (such as copper or optical cable)
• [TX] Encodes data into a transmission signal supported by the medium
• [RX] Decodes data into a transmission signal supported by the medium
• [TX+RX] Generates or amplifies re-transmitted signals along the medium
• [RX] Monitors (only detects) transmission errors
• [RX] Detects arriving signal levels to synchronize speed and timing

Data Link Layer responsibilities:

• [TX] Constructs data frames using the format of the Physical Layer
• [TX] Calculates Cyclic Redundancy Codes (CRC) information
• [RX] Checks for arriving errors using CRC information
• [RX] Initiates and arbitrates the link to reduce interruption and contention
• [RX] Examines arriving and passing device addresses in data
• [RX+TX] Acknowledges receipt of a frame
• [RX+TX] Retransmits data if there is an error

Metrics Of Network Measurement

There are two components to performance - latency and bandwidth. We always want high bandwidth and low latency, but can't always get both together.

• Latency or propagation delay is the amount of time it takes for the first bit to reach its destination. Round-trip time (RTT) is (naively) twice the latency - the time for one bit to travel to the destination, and the first bit in reply to return.
• Bandwidth is the number of bits that can be fit through a network connection, per unit time. Historically, i.e. without any data compression, bandwidth has been related to frequency within the medium.
• Throughput is usually the measured number of bits per second (achieved), while bandwidth is the nominal (peak) number of bits per second possible. High bandwidth does not imply low latency: you can broadcast many Mbps over a satellite connection, but it will take hundreds of milliseconds to arrive.

The latency of a message is the total time for the whole message to arrive:

    TLatency     = TPropagation + TTransmit + TQueue

    TPropagation = distance / speed-of-propagation-in-medium
    TTransmit    = message-size / bandwidth
    TQueue      = time-spent-in-local-and-remote-operating-system-and-switch-queues

On prefixes

See: Transmission time [Wikipedia], Binary prefix [Wikipedia], and Grace Hopper Explains a Nanosecond.

The Physical Layer and Transmission Errors

Rates of transmission errors are described by their probability of occuring, or by their expected bit-error-rate (BER).

Transmission errors usually occur in bursts and are caused by:

• Thermal background noise
• Impulse noise, electrical arcing (~10ms duration)
• Distorted frequency
• Crosstalk between adjacent wires

Over a particular time interval, a burst begins at the first bit that is corrupted (inverted), and ends at the last bit corrupted - the bits between are not necessarily all modified.

Discussion question 1

Never underestimate the bandwidth of a station wagon full of tapes hurtling down the highway. Andrew Tanenbaum - "Computer Networks" 3rd ed., p83

Order the bandwidths of the following "communication technologies", and the times taken to perform each transfer: Australia Post delivering a movie on DVD overnight (olde NetFlix), transferring a large 100MB file over the UWA wireless network, copying the same 100MB file from a hard disk drive (HDD) to the same disk, copying the same 100MB file to a USB drive, copying one 1MB array to another in a high-level programming language, refreshing the screen of an ASCII terminal using a 56Kbps modem, transmitting an A4-sized FAX in 30 seconds, and transmitting data across a Bluetooth network.

How Data is Placed in Frames

Simple timing gaps between frames cannot be used as all hardware devices (as part of the Physical Layer) run at slightly different speeds; resulting in skewing if time is relied upon.

A first attempt at a solution involves counting the size of a frame and placing this count in the data link header - blah!

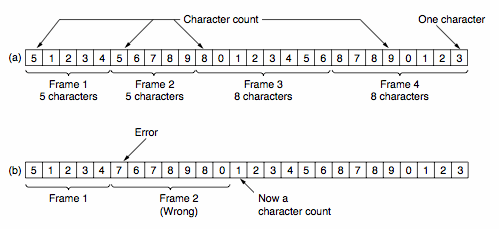
This naive solution highlights problems with synchronization - assuming the receiver can detect a problem, how much of the arriving bit stream should be skipped to find the next frame?

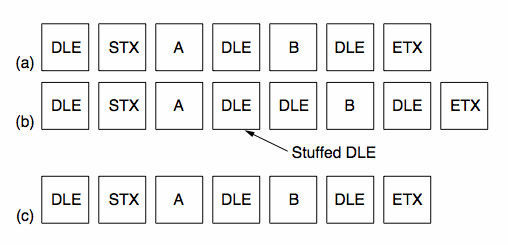
How Data is Placed in Frames, continued

To overcome synchronization problems, special byte sequences are often used to prefix and suffix (envelope) the data.

As these special bytes may themselves be required data we must "escape" their special meaning (particularly true for "binary" data such as floating point numbers, executables, JPGs and MP3s).

This process is termed byte stuffing, using DLE=020₈, STX=002₈, ETX=003₈.
On a Linux or macOS machine, execute: man ascii.

Consider the following example, transmitting 3 bytes: [A, DLE, B]

A lower-level approach, bit-stuffing, overcomes the reliance on using the ASCII codes. Each frame is now enveloped in pairs of "flag" patterns 01111110.

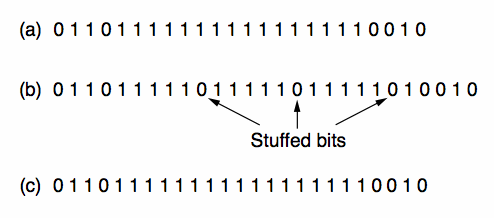
If this flag pattern appears in the data, the stuffed sequence 011111010 is transmitted.

Phase Encoding of Signals

To be able to detect collisions on LANs, we need to understand how digital signals are encoded on the physical medium.

A digital signal is a sequence of discrete, discontinuous pulses, or signal elements.

If all signal elements have the same (voltage) sign, they are termed unipolar.

The modulation rate of a LAN is the number of signal elements (transitions) per second, or the baud rate.

To correctly interpret a signal, the receiver must know the length (time) of each signal element and the expected voltage levels of the bits 0 and 1.

The two simplest encoding schemes are the:

• Non-return to Zero Level (NRZ-L) and
• Non-return to Zero Inverted (NRZ-I).

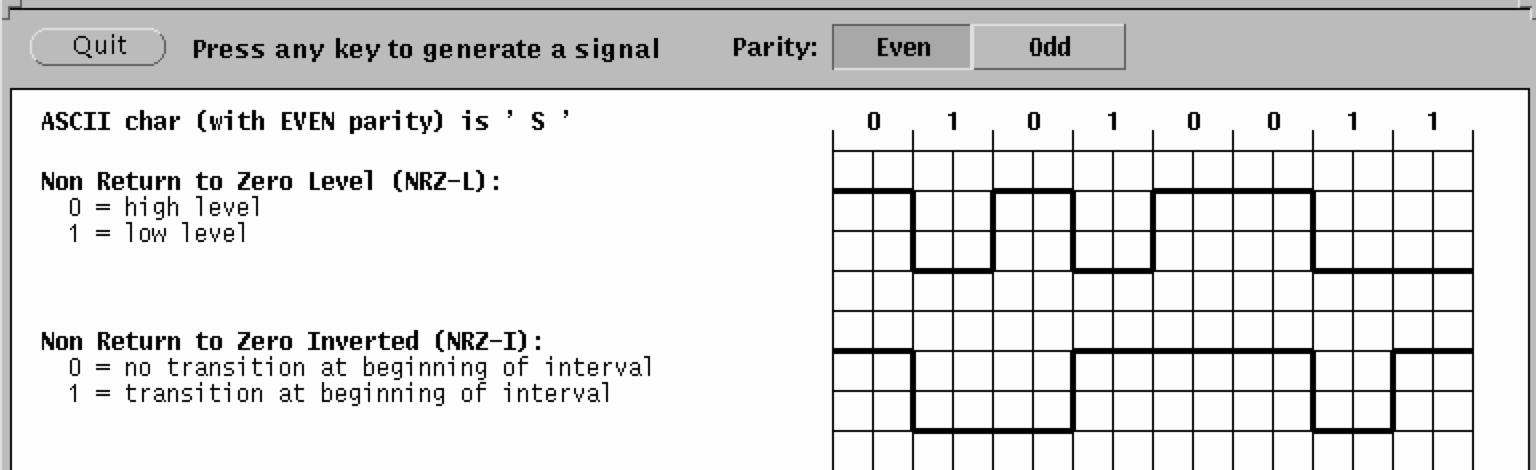
NRZ-I is an example of differential encoding in which the signal transition, rather than the signal level, indicates the value of each bit.

See also: Sound of the dialup modem explained.

Phase Encoding of Signals, continued

NRZ-L and NRZ-I are simple schemes, but unfortunately offer no possible synchronization.

Another scheme, biphase encoding, ensures that there will be a transition in the middle of each bit.

With Traditional Manchester encoding the mid-bit transition provides a clocking mechanism (as well as the data).

With Differential Manchester the mid-bit transition provides the clocking and the initial transition provides the data.

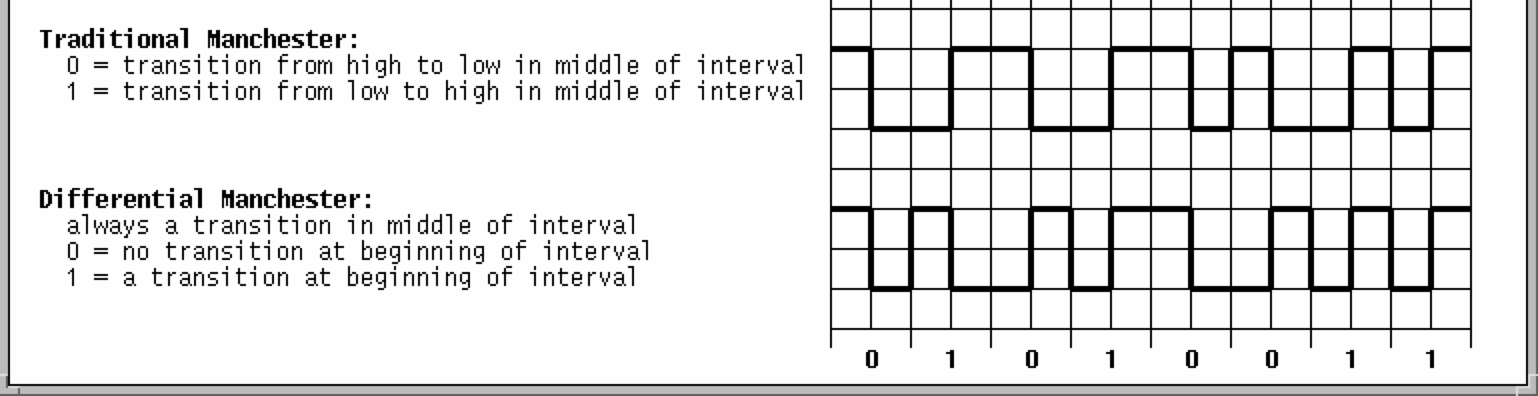
Biphase encoding schemes have (at least) one transition per bit time, thus the maximum modulation rate, or baud rate, is twice that for NRZ-L and NRZ-I.

Error Detection and Correction

Data may be modified so that errors can either be:

• detected (i.e. you can only tell that the data is wrong), or
• corrected (i.e. you can unambiguously tell what the data should have been, and hence you can confidentially correct it).

Correction is required where communication must be simplex (only possible in one direction), but correction is expensive. A good example of its need is between Earth and inter-planetary spacecraft. Error correction by the receiver is referred to as forward error correction, whereas re-transmission schemes are referred to as reverse error correction.

Codewords are constructed consisting of both data and check bits.

The Hamming distance between two codewords consists of the number of bit positions in which they differ.
The difference is performed Modulo-2 or EXCLUSIVE-OR:

e.g.	1 ⊕ 1  =  0 ⊕ 0  =  0
	1 ⊕ 0  =  0 ⊕ 1  =  1

	 10011101
	 10111110
     --------------
       ⊕ 00100011

Here, the Hamming distance is 3.

The Hamming distance of a code is the minimum Hamming distance between any two words in that code.

Error Detection and Correction, continued

To detect: δ errors, a distance of δ + 1 is required.

e.g. to detect 1 bit in error requires that there is no word with a distance of 1 from a valid word.

To correct: δ errors, a distance of 2 δ + 1 is required so that even with δ errors, the damaged codeword is the closest to one valid codeword.

Some examples :

Consider a simple encoding of ASCII characters, where we use a parity code [see Tanenbaum 5/e]
We have 7 data bits and a single parity-code bit. Now, what happens if any single bit is corrupted?

• What is the distance of the parity-code?
• What type of errors can it detect?
• What type of errors can it correct?

Consider a code whose only valid code words are :

    0000000000  1111100000  0000011111  1111111111

• What is the distance of this code?
• What type of errors can it detect?
• What type of errors can it correct?

Hamming's Correction of Single-Bit Errors

Let's say that a single transmission consists of m bits for the message, and r bits of seemingly redundant information.
We thus transmit n = m + r  bits when transmitting a message.

The critical question is "how much additional information (the redundant bits) do we need to transmit so that the receiver can correct errors?"

Each of the 2 ^m possible message words has n illegal code words which are a distance 1 from it. Therefore each message word requires n + 1 distinct bit patterns (1 legal one, and n illegal ones).

In 1950, mathematician and Turing Award winner Richard Hamming developed a method which achieves the lower bound of:

Given a code word of 7 data bits and 4 check bits, we number the code word from 1 from the left hand side.

Each bit whose ordinal position is a power of 2 {1,2,4,8,...} is a check bit and forces the parity of some "collection" of bits including itself. Parity may be forced to be either even or odd.

Hamming's Correction of Single Errors, continued

A data bit contributes to the parity of all bits in its decomposition into a sum of powers of 2.

For example :

     3 = 2 + 1
     7 = 4 + 2 + 1
    11 = 8 + 2 + 1

Making a list of these :

    1 is contributed to by 3, 5, 7, 9, 11
    2                      3, 6, 7, 10, 11
    4                      5, 6, 7
    8                      9, 10, 11

We then put the data bits in their positions and calculate each check bit.

Hamming's Correction of Single Errors, continued

For example, ASCII character 'c' = 1100011, using even parity :

         1  2  3  4  5  6  7  8  9 10 11
        ---------------------------------
               1     1  0  0     0  1  1


check 1        X     X     X     X     X

check 2        X        X  X        X  X

check 3              X  X  X

check 4                          X  X  X

The resulting codeword is hence 11111000011.

We then transmit this codeword across the network.

Hamming's Correction of Single Errors, continued

When a codeword is received at the other end we must check (and possibly correct) it.

To correct when it arrives:

Initialize a counter, c, to 0.

Examine each check bit in position k={1,2,4,8} to see if it has the correct parity.

If not, add k to c.

When all check bits have been examined, and counter c is 0, then codeword is correct. Otherwise, the incorrect bit is in position c.

For example, if we transmit 11111000011 (from before), but we receive :

      1  2  3  4  5  6  7  8  9 10 11
     ---------------------------------
      1  1  1  1  1  0  0  0  0  1  0

c=0
k=1	parity for 3,5,7,9,11	wrong! so  c+=k  (=1)
k=2	parity for 3,6,7,10,11	wrong! so  c+=k  (=3)
k=4	parity for 5,6,7	correct
k=8	parity for 9,10,11	wrong! so  c+=k  (=11)

Hence bit 11 is in error!

Cyclic Redundancy Codes (CRCs)

The extra bits used to detect errors are called checksum bits.

A checksum can be quite simple, for example "add-with-carry" all bytes in a message, or much more sophisticated as in the case of a cyclic redundancy code (or CRC).

Polynomial Codes

A polynomial is represented by a bit string with 1 for each power represented in the polynomial, and 0 otherwise.

e.g. x⁴ + x³ + 1 is represented as 11001

Polynomial arithmetic is performed Modulo-2 or EXCLUSIVE-OR

e.g.	1 ⊕ 1  =  0 ⊕ 0  =  0
	1 ⊕ 0  =  0 ⊕ 1  =  1

Both the sender and receiver agree on a generator polynomial, G(x), with high and low order bits 1.

The message, M, is also interpreted as a polynomial.

The checksum (when calculated) is appended to the message so that (M + checksum), known as the transmission T(x), is divisible by G(x).

On arrival we simply check that the received transmission is divisible by G(x).

[See A Painless Guide to CRC Error Detection Algorithms]

For examples of other types of checksum algorithms, see the Australian Securiities & Investment Commission and
the Australian Tax Office, (or on GitHub).

Polynomial Codes, continued

What types of errors can (and cannot) be detected with CRCs?

Let the error bits in T_arrived(x) be E(x). Each bit in E(x) corresponds to a bit that has been inverted.
If there are k 1 bits in E(x), then there have been k single-bit errors.

Then, due to the properties of the Modulo-2 arithmetic:

    (T(x) + E(x)) / G(x) = (T(x) / G(x)) + (E(x) / G(x))
                         =       0       + (E(x) / G(x))

We notice that if G(x) divides E(x) (because G(x) is a factor of E(x)), then errors can go by undetected.

Some important results:

• If G(x) has two or more terms all single bit errors can be detected.
• To detect double errors, G(x) must not be divisible by ( x ^k + 1) for k up to some maximum frame length.
• To detect an odd number of errors, G(x) should contain (x+1) as a factor.
• Polynomials of degree r will detect all burst errors of <= r bits.

Some Standard Polynomial Codes

16 bit checksums catch -

• all single and double bit errors
• all errors with an odd number of bits
• all burst errors ≤ 16 bits long
• 99.997% of burst errors = 17 bits
• 99.998% of burst errors ≥ 18 bits

   CRC-12 = x 12 + x 11 + x 3 + x 2 + x + 1

   CRC-16 = x 16 + x 15 + x 2 + 1

CRC-CCITT = x 16 + x 12 + x 5 + 1

   CRC-32 = x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 +
            x 8 + x 7 + x 5 + x 4 + x 2 + x + 1

CRCs are often performed in hardware, for example the DEC-VAX architecture (mid-1980s) had an assembly language instruction to perform CRC-16 (!).

Today, all network interface cards (such as wired and wireless Ethernet) perform checksumming "on-board".